
In this part, you will use Bayesian statistics to improve the performance of A/B testing using your prior knowledge. The next part will extend the concepts of Bayesian statistics to create an intelligent campaign and digital marketing design. This is kind of similar to creating an artificial intelligence for the purpose.
Before we start our case study example, let’s understand the underlying principals of Bayesian thinking and statistics.
Bayesian Statistics to Improve A/B Testing
Bayesian statistics may seem intimidating to many but the ideas behind Bayesian thinking are extremely intuitive and simple. For me, this quote by Isaac Newton captures the essence of Bayesian thinking.
If I have seen further than others, it is by standing upon the shoulders of giants.
– Isaac Newton
Newton was referring to giants like Galileo, Copernicus, Aristotle, and many others for his work on celestial motion and gravity. It makes sense because learning and knowledge are incremental processes. Even the greatest scientists use the work of their predecessors to develop new theories and knowledge. The next generation is usually an extension of the previous generations.
You may find it surprising that the prevalent methods for analysis don’t work in a similar incremental fashion of building on top of the existing knowledge. These methods are based on Fisherian statistics aka the frequentist approach. In the frequentist approach, each analysis is an isolated island and it is left to humans to make the connections between different analyses. Traditional A/B testing or hypothesis testing is a form of the frequentist approach. Bayesian statistics, on the other hand, use priors similar to how Newton used the works of other scientists prior to him. Bayesian statistics incorporate the prior knowledge and the new evidence (data) to generate new knowledge. This new knowledge is known as posterior in the Bayesian parlance.
Despite being intuitive, the biggest challenge for Bayesian statistics is that, unlike traditional statistics, it is computationally expensive. This means that Bayesian statistics requires higher computation power for some of its applications using Markov Chain Monte Carlo methods (MCMC). We will explore MCMC in some other posts on YOU CANalytics. For now, let’s explore methods that make Bayesian calculation less expensive and easy to implement i.e.
Conjugate Priors
Let’s try to understand conjugate priors in an intuitive way. Look at this illustration:
Conjugate priors (read prior probability distributions) form a harmonic relationship with the distributions of data (evidence) to produce easy to decipher posterior distributions. This is similar to mixing distilled water from two different rivers and getting more distilled water which has the same properties as the prior distribution. Non-conjugate priors, on the other hand, is like mixing soil and water. In this case, the posterior is like sticky mud which is hard to work with.
If we work with conjugate priors, our job with Bayesian inference becomes quite easy and less computationally expensive. For non-conjugate priors, we use computationally expensive methods such as Markov Chain Monte Carlo (MCMC).
In this case study example, you will work with the conjugate prior of the email campaign performance. You had identified the click rate as the performance metric for success of the digital ads. A click is a binary event that can have just two possible values i.e. clicked or not clicked. Such binary events are described as Bernoulli experiments. Yes, the famous coin tosses are also Bernoulli experiments as are so many other applications in business.
For clicks, the likelihood or evidence/data distribution of Bernoulli experiments is defined by this function.
Here, θ is the real click rate. Bernoulli experiments take Beta distribution as the conjugate prior.
Beta Distribution – Conjugate Prior for Click Rate
If you are panicking at the mention of beta distribution, I could totally understand. But trust me, it is a really cool function. The shape of a beta distribution depends on the values of two constants α and β. Different values of α and β produce different shapes of probability distributions. Moreover, a beta distribution always lies between the value 0 and 1. This is perfect for us since click rate also always lies between 0 and 1.
Here, B(α,β) is a constant to normalize the distribution. In this diagram, 4 different beta distributions are displayed with different values of α and β.
You must have noticed how beta distributions starts to look like a bell curve or normal distribution as the value of α and β starts to get bigger. Also notice that with the greater values of α and β, the bell curves are getting thinner or have smaller standard deviations. Now, let me reveal the coolest property of beta distributions for prior and posterior probabilities when the data is obtained from a Bernoulli experiment. Remember, prior is old knowledge and posterior is new knowledge in presence of new evidence or data. For click rates, p(θ) is the prior probability; p(#Click|θ) is the probability of the evidence with the given prior or θ; p(θ|#Click) is the posterior probability. Bayes rule creates a straightforward multiplicative relationship between prior, evidence, and posterior as:
The posterior, thus, can be approximated by p(θ) and p(#Click|θ) equation discussed earlier.
This is simplified to:
Notice, the posterior in this case is another beta distribution. The posterior beta distribution has a very simple relationship with the prior and number of clicks!
We will experience the power of this simple equation in the next segment when we will go back to our digital marketing case study example.
Digital Marketing – Case Study Example
In this case study example, you are helping your client to improve their digital marketing efforts. Your client is a charity organization that is working on an email campaign to ask people to donate money to the needy in Africa. These are the three ads that they had sent across to three different sets of recipients. The performance measure, as discussed in the last post on A/B testing, is the click rate. Before you read further, just look at these 3 ads and decide which one will perform better than others.
You are an expert in digital marketing and advertising. In your experience, you have noticed that ads with humans perform much better than ads with abstract images. The abstract image, in this case, is the map of Africa in A. Your opinion is that ad C will outperform ad B and A. Also you believe, B will do better than A.
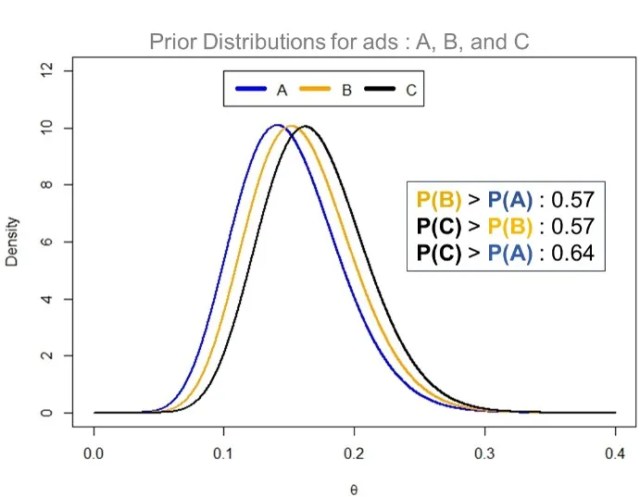
Prior Distributions – Old Knowledge
You expect click rate for C to follow a bell curve with the mean of 17% and standard deviation of 4%. Similarly, you expect A and B to have the respective mean click rates of 15% and 16%. They also have the standard deviation of 4%. This expert opinion (bell curves or normal distributions) can be easily approximated as beta distributions as displayed in the graph below.
You could find the complete R Code for Bayesian AB Testing on this link. All the plots and analyses to follow are captured in this code.
These 3 prior distributions for ad A, B and C are beta distributions (they look identical to bell curves assumptions you had made). For ad A, you had estimated α = 11.8 and β = 66.9 to produce the beta distribution with the assumption of a bell curve with the mean of 15% and sd of 4%. Similarly, ad B has α = 13.3 and β = 69.7. Moreover, ad c has α = 14.8 and β = 72.4. You could get these numbers by running the R-code I had shared earlier.
You have also estimated with the help of Monte Carlo simulation that ad C will outperform B in 57% cases. Similarly, C will do better than A for click rates in 64% cases. This prior information is not good enough for you to be conclusive about the performance of these ads. This is precisely the reason you why had launched this campaign/experiment with these ads being tested on a large number of recipients.
Posterior Distribution – New Knowledge in the Presence of New Evidence (Data)
If you recall, last week the IT team of you client shared these results for the click rate in the first hour after the launch of the campaign.
| Ads | Total Emails Sent | Clicks (1st hour) | Opens (1st hour) |
| A | 5500 | 4 | 58 |
| B | 9000 | 14 | 101 |
| C | 12500 | 23 | 129 |
Here for ad A, you didn’t have a big enough sample of clicks, just 4, to use them for A/B testing by the frequentist approach. Bayesian A/B testing, however, because of the prior (old knowledge), can still incorporate these samples to produce meaningful results or the posterior distribution (new knowledge).
You easily incorporated these results in the prior beta distributions (old knowledge) to produce the posterior distributions (new knowledge) with the formula we discussed in a previous segment on beta distributions. For ad A, #click or number of clicks = 4. Similarly, #No click = 58-4=54.
Similarly, you had calculated posterior β for ad A as shown below.
You did the same calculation for other posterior distributions of B and C as well. Once you knew the parameters (α and β) for the posteriors, you easily plotted the beta distributions for posteriors.
In this case, B is performing better than A in 81% cases. Already, with the limited sample size, we have an improvement on our priors (old knowledge). C will outperform A in 94% cases. Hence, with the new evidence, it is safe to say that Elisa is receiving higher empathy from the recipient of the emails then the map of Africa.
Posterior Distributions after 5-days
After collecting data for five days you had all the possible results from the campaign. These were the results you had seen in the previous part as well while doing A/B testing by the frequentist method.
| Ads | Total Emails Sent | Clicks (5 days) | Opens (5 days) |
| A | 5500 | 41 | 554 |
| B | 9000 | 98 | 922 |
| C | 12500 | 230 | 1235 |
Using this new and improved evidence, you calculated the new beta distributions for the click rates for the 3 ads.
Now, you know almost conclusively that ad C had outperformed both ad B and A in terms of click rates. You could create new sets of experiments with variants of ad C to further improve the performance on the click rates.
Sign-off Note
You showed your results for the click rates to your client. She found it useful. After looking at the results one more time, she said -“As an organization, we care more about donation amount and not so much about the click rates”. She is a smart woman and even though you are doing this work for free or pro bono, she will not shy away from asking the right questions.
Incidentally, you had thought of these issues and designed the campaign accordingly. You reminded her that in the previous part of this case study, she had asked you another question about the disproportional distribution of email recipients across the 3 ads. She noticed that you had identified 5500 recipients for ad A and 12500 recipients for ad C. You told her that both her questions about maximizing the donation amount and the disproportional distribution of recipients are actually linked. You promised her that you will reveal the link in the next part of the case study. Moreover, you also promised that you are developing an intelligent campaign design for her that will learn from the previous campaigns to generate maximum returns in the form of donations.
She was excited to learn the links between her questions and also to identify digital marketing ways to generate the maximum donation to help the needy in Africa. She immediately marked a date in her busy calendar to learn all this.








Very cool analysis and nice (and fun, and enjoyable) explaination.
I only miss one detail: when you define the priors, how do you come up with those exact numbers for the click rates in cases A, B and C (means and variance for Normal distributions)? How one is supposed to get them from the previous analysis?
That is a very good question because prior separates Bayesian from Frequentist. In this case, the prior distributions were derived from historic information (past data) about the campaign metrics coupled with experts’ opinion.
To elaborate, click and open rates usually follow an expected distribution for most campaigns. For instance, they are almost never above 40-50% range for a mass marketing effort like this one. Moreover, you don’t expect these metrics to fall below 2-3%, like ever. These metrics ranges are usually follow an expected distribution and an experienced professional can easily see through the segment of the campaign (nature, industry, message, creative quality, targeted audience etc.) to further refine prior distributions – as we did in the case study example. If these is no information and expert guidance available then one could use an uninformative prior of 0-50% for these metrics – this is still better than searching for your answer in the complete 0-100% range.
Hi Roopam,
Thanks for this – big fan!
I have a question(am at beginner stage), when we represent the beta distributions of prior or post probabilities, how do you say that B performed A by x%. Is it something that is derivable from the output by laying out beta distribution from code? How do we derive the x% here?
p(\#Clicks|\theta )=\theta ^{\#clicks}(1-\theta)^{\#No\ clicks}
Here, θ is the real click rate. Bernoulli experiments take Beta distribution as the conjugate prior.
Got stuck here. Can you please explain
Is it okay to assume that C, A, B have means of 17%, 15%, 16% but standard deviation same as 4% since mean for Bernoulli is p and standard deviation would be p(1-p). Shouldn’t it be 38%, 36% and 37% respectively?
These are prior distributions derived from prior experience. Bernoulli variances are not applicable here.