How do machines learn? They learn the same way as humans. Humans learn from experience and so do machines. For machines, the experience is in the form of data. Machines use powerful algorithms to make sense of the data. They identify underlining patterns within the data to learn things about the world. Like humans, machines use this learning to make decisions. For example, amazon.com uses machine learning to recommend products to you based on your surfing patterns on their website. Forrester Research estimates sales conversion through this recommendation engine as high as 60%. Companies across the globe are making huge profits through decision making by machine learning algorithms.
Many powerful machine learning algorithms use gradient descent optimization to identify patterns and learn from data. Gradient descent powers machine learning algorithms such as linear regression, logistic regression, neural networks, and support vector machines. In this article, we will gain an intuitive understanding of gradient descent optimization. For this let’s take a dive towards these concepts with some help from…
Gravity
A few years ago my wife told me this incident about her friend who has a young daughter. One day my wife’s friend discovered that her young daughter had dropped and broken a lamp while playing. When she inquired from her daughter about how that happened, the little girl responded: “Grabili did it, mommy, it’s not [entirely] my fault, it’s Grabili”. The girl was referring to gravity and she was right that gravity was an equal accomplice in her mischief. Like the little girl, we all know through the works of Galileo and Newton that gravity is responsible for everything that falls.
Gravity has important lessons that will help us gain an intuitive and simplified understanding of gradient descent.
Gravity & Gradient Descent Optimization
Consider these 3 situations where a ball is placed in a glass bowl at 3 different positions. We all know through our experience with gravity that the force of gravity will pull the ball towards the bottom of the bowl.
In situation 1, the ball will move from position b1 to c1 and not a1. This ball will continue to travel till it reaches the bottom of the bowl. In situation 2, since the static ball is already at the bottom it will stay at b2 and it won’t move at all. The ball always tries to move from a higher potential energy state to a lower. Gravity is responsible for these different potential energy states of the ball.
Now, you must ask: how is this similar to gradient descent optimization? Actually, this is exactly how gradient descent optimization works. The only major difference is that gradient descent optimization tries to minimize a loss function instead of potential energy.

Also, notice that the ball experienced different pulls at different stages while it journeyed towards the bottom of the bowl. These pulls can be evaluated through the gradient or the slope of the orange arrows shown in the adjacent picture. The steeper the orange arrows larger is the force of gravity on the ball.
For gradient descent optimization, the z-axis is the loss function and x & y-axes are the coefficients of the model. The loss function is equivalent to the potential energy of the ball in the bowl. The idea is to minimize loss function by adjusting x & y-axes (i.e coefficients of the model).
If this sounds a bit vague wait till we will solve an example of a linear regression model later in this article. But before that let us refresh a few concepts from high school mathematics involving differential calculus and finding the minimum value for a function.
Gradient Descent – Finding Minimum Value of a Function
There are essentially two methods for identification of minimum value for a function. We will explore both these methods in this section. This will pave the way for us to understand gradient descent. Let us consider the following function and identify the minimum values or minima for the function.
This is the plot for the above function with different values of x.
As you must have noticed, point a and c are the bottom points or minimum values on this curve. Now we want to find the values of point a and c through two different methods i.e. logical and numeric/iterative solutions.
Method-1: Differential Calculus
The first method is a logical method which requires solving an equation. We can find the minimum or maximum values for this function at the points where the gradient or the slope of the function becomes zero similar to the bottom of the bowl. Mathematically, this expression is obtained by equating the first differential of the function to zero as shown below:
If we will solve this equation we will get ±√5 as the value of x where this function has the minimum values.
This makes sense since even if we look at the plot the minimum value for x is slightly away from x= ±2.
Method-2: Iterative Calculation
It is great to solve the equation with the first method but unfortunately for quite a lot of complicated functions, it is not possible to solve equations the way we do in method-1. Hence we need to identify some numeric methods to solve such equations. Numeric methods to solve an equation require iterative calculation. It is similar to rolling a ball downwards, and measuring its position with each calculation till it reaches the bottom. The idea is to measure the speed of the ball based on the gradient or the slope of the curve. This is precisely how gradient descent optimization works.
The first thing you must have noticed is that this function has 2 minimum values. Hence, initial positions of rolling the ball will take you to different values ( √5 or -√5). This is a slight problem but luckily for many machine learning problems we just have one minimum value. This special property of a function is referred to as convexity. In other words, convexity is the property of a bowl to have just one bottom.
Moreover, to roll the ball we need to know the gradient or slope of the function (bowl) at different points. But how does one identify gradients of the curve at different points? We will learn this in the next segment by solving an example for linear regression.
Linear Regression – Loss Function & Gradient Descent
There are several business problems that use linear regression to estimate values. For instance, if we have data for 100 professionals about their salaries and years of experiences we can fit a curve on this data and identify patterns between these two variables. Using the data we are trying to estimate an equation of this nature:
Now, if some professional tells you she has 10 years of experience. You could easily estimate her salary as 70,000 (5000×10+20000). The most important factors here are the values of the coefficients for the line (i.e. m = 5000 & c=20000). We can estimate these coefficients with the data through either the Ordinary Least Square (OLS) Method or gradient descent optimization. This example is quite simple but imagine if you had 8000 more variables in addition to years of experience that’s when you need machine learning and gradient descent.
Let me tell you upfront that gradient descent is not the best way to solve a traditional linear regression problem with fewer predictor variables. Linear regression models could be solved for their coefficients more efficiently through the Ordinary Least Square (OLS) method. OLS is kind of like method-1 in the previous section i.e. more straightforward. Gradient descent, on the other hand, is like method-2 and requires iterative calculation.
Despite inefficiency, traditional linear regression offers an easier way for us to understand gradient descent. More importantly, non-traditional regression in machine learning with thousands of predictor variables involves linear regression with regularization (i.e. ridge regression and lasso). These linear regression models with regularization coefficient are efficiently solved using gradient descent method.
OK so now let’s move to our example with simulated data for x and y (similar to years of experience and salary). Consider this data set with different values of x and y. We will try to find the equation of the orange line through both OLS and gradient descent methods.
Method-1: Solving Linear Regression by OLS
We are interested in finding an equation for the line through linear regression.
Here, m and c are constants or coefficients of a regression equation.
As discussed earlier, we can easily solve this linear equation with OLS. Using R’s lm function we get this equation of the line for our data (m = 1.013 & c=1.003). Lm function uses matrix inversion. R code for linear regression.
Method-2: Solving Linear Regression by Gradient Descent
Now, let’s try to find the values of coefficients (m & c) using gradient descent. For this first, we need to identify the error or the loss function for the linear regression model. Remember the loss function will determine the shape of the bowl on which we are rolling the ball. The generalized equation of loss function for any problem is:
This is the original value of y minus expected value. For the linear regression problem, the expected value is the equation of the line, therefore:
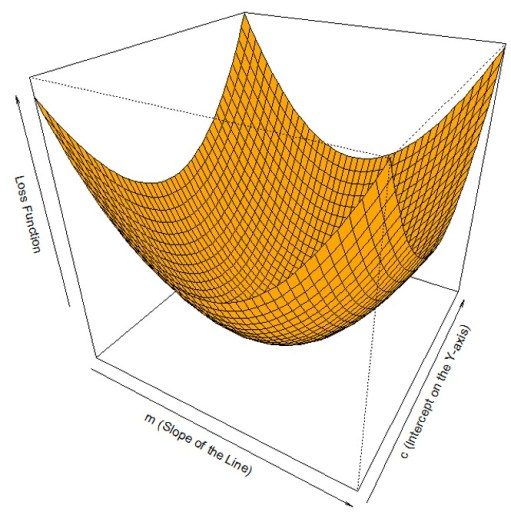
If we plot loss function (z-axis) with respect to the coefficients of linear regression (m and c) the 3D plot looks like this.
Alright, this looks like a bowl. Now, we just need to roll down the ball to identify the minimum value of loss function by adjusting the coefficients (m and c). Gradient descent reaches the bottom of the curve by iterative calculation of both m & c. For this, we need to figure out the way to roll the ball down the slope at each step. Keep the following analogy between gravity and gradient descent which minimizes loss function by adjusting for m & c.
| Gravity Analogy | Gradient Descent |
| Potential Energy | Loss Function |
| Objective: Minimize Potential Energy | Objective: Minimize Loss Function |
| Horizontal Plan (X & Y Axes) | Regression Coefficient (m & c) |
| Modify X & Y to Achieve the Objective | Modify m & c to Achieve the Objective |
| The shape of the Bowl | Relationship btw Loss Function, m, & c |
| Bottom of the Bowl | Minimum Value of Loss (Error) on LF |
Firstly, gradient descent requires the direction of the downward slope at each point on the loss function with respect to both m & c. Secondly, it needs to control the speed at which the ball will roll. This entire thing is captured in this equation for m:
Here, the new position of m i.e. (mn+1) is decided by the previous position of m i.e. (mn) by rolling the ball down the slope ( ) . The partial differentiation term determines the gradient or slope of the curve. Additionally, α is learning rate which determines the speed at which the ball will roll.
Similarly, we can iteratively estimate the value of the other coefficient of the linear regression model i.e c. The best fit value for c and m is when the slope becomes flat or the ball gets to the bottom of the bowl.
Now we just need to find the gradient term and supplement them in the above equations. The gradient term for m is:
Similarly, the gradient term for c is:
Finally, we choose the constant value for learning rate (α) as 0.01. We are now ready to run the gradient descent optimization to find values of m & c through iterative calculation. This R code for gradient descent captures all the equations discussed above and does the iterative calculation for m & c to minimize loss function. Gradient descent optimization gives the same value for the coefficients as OLS i.e. m = 1.013 & c=1.003. Please run the code and check for yourself.
The following heat map points to the value of loss function for different values of m & c. As expected, this points to the minimum value at m = 1.013 & c=1.003.
Sign-off Note
So gravity and gradient descent have so many similarities. Next time when you see something falling, do think of gradient descent. A question you may want to ponder: does nature do so many iterative calculations to make things fall?







Fantastic post! Congrats Roopam!
Thanx for taking time to explain this
Analogy between nature and science is the key of learning .
Earlier I found little difficulty to understand intuition behind the Gradient decent. It’s explained in very simple way..Thanks Roopam.
If you get a chance, kindly provide intuition behind Local optima and Global optima and How to Identify if we have reached global optima or local optima..Thanks in advance
-Pavan
Thanks Pavan, I appreciate that.
To understand global optima i.e. maxima / minima let us consider the function that we have discussed in this post
For this function point b is a local maxima. How do we know that? Because between points a and c that is the maximum value for the function. However, unless we go beyond these points there is no way for us to identify that it is a local maxima. For this function a global maxima is infinity since the value of function will continue to rise till eternity with an incremental value of x. Hence, there is no way for us to estimate that with both the methods we have used to find optimal value of the function.
Method-1 uses differential calculus to identify all the points where the slope of the function becomes zero. However, for a continuously increasing / decreasing function we won’t find the maxima or minima with this method since it is plus / minus infinity.
Method-2 and gradient descent method have a bigger challenge since the rolling ball will just stop at any point where it finds a flat surface. One of the practical solutions for this is to make the ball roll from different initial points and hope that you have arrived at the minima. Luckily for the optimization problems with squared error function there is just one minima.
Hi:
Gradient descent sounds like a variation of a linear programming algorithm.
Regards,
Jay
That’s true Jay, gradient descent is a minimization problem subjected to model constraints hence it is similar to linear programming (LP). For fewer predictor variables you could also use Excel Solver (optimization) to build linear or logistic regression models. However for a large number of predictor variables, common in machine learning problems, gradient descent works better.
Hi dear Roopam
great explanation, huge thanks
but i have one query, so after so many iterations for finding lowest point of the gradient descent
how do you understand that lowest point is reached.
i.e 1. m=5, c=4
2. m=4.9 c=3.9
3. m=4.7 c=3.7
–
–
–
m=0.5 c=0.6
when should i stop understanding that optimal minimum is reached
what is the signal or value that gives me the lowest point.
At the optimum or minimum value for the loss function, the gradients d(LF)/d(m) and d(LF)/d(c) become zero. This also indicate that your ball has reached the bottom of the bowl since the slope is zero. In practice, you could check if the gradients are less than a certain threshold say 10^-6 before stopping the algorithm.
Roopam,
Apologize if my questions sounds naive. The gradient descent algorithm finds the coefficients (m and c here) that provides the local optima. For this purpose, we start with an arbitrary coefficient values and reduce them till the lowest point is reached. Will the coefficient values get close to zero always to achieve local optima? If so, why don’t we start the gradient descent search with m=0 and c=0 and increase gradually?
Since we are working with a convex loss function, gradient descent, in this case, will always find global optima. Remember, a convex loss function is shaped like a bowl and has just one minimum value.
The coefficient values don’t necessarily get close to zero – there is no such condition and the coefficient values depends on the dataset. One of the approaches is to normalise the dataset to keep the coefficient values in a relatively narrow range but again no reason to believe that they will converge closer to zero.
Excellent and very easy to understand explanation. Thank you.
ખૂબ સરસ
ખૂબ સરસ સમજ આપી છે
Hello. Thank you very much for this post. I have a hard time understanding mathematical concepts, and this helped me a lot in studying for my Machine Learning exam. Thanks! 🙂
but I have a question “where is the minus” that is with -mx because the equation is “y-mx-c”
please answer it <3 ?
Not sure if I have understood your question completely. Are you talking about this equation?
This one has the same form as you expected, notice the brackets.
Thankyou Roopam this is very helpful
Dear Roopam, thanks for an easy explanation. Could you tell me the difference between this method and ‘steepest descent method’ of geometry optimization?
Regards,
Thanks. To answer your question, the method of steepest descent is also called the gradient descent method. In computer science and machine learning, you will almost always refer to the method as gradient descent.
Roopan, Thanks my brother. The great ones make it look easy:)
Confusing. Isn’t it true, the algorithm (Newton/Newton-Raphson) is equally efficient in gradient accent also, against the gravity! It is just taking advantage of the information in the behaviors of the gradients to go to the minimum or maximum.
Thanks for trying to make it easier for people to understand. Best.