This is a continuation of the banking case study for the creation of application risk scorecards we have discussed in some previous articles. You could find the previous parts of the series at the following links (Part 1), (Part 2), (Part 3) and (Part 4).
In this article, we will discuss the Population Stability Index (PSI), an important metric to identify a shift in population for retail credit scorecards. Before we delve deeper into the calculation of the population stability index (PSI) and its utility, let’s try to understand the overall purpose of the PSI and similar indexes by connecting a few dots between..
Dictators and Credit Crisis
What is similar between Napoleon’s and then Hitler’s attempts to invade Russia and financial crisis of 2007-08?
Napoleon tried to invade Russia in 1812 and Hitler repeated Napoleon’s misdeeds in 1941 – both invasions ended with severe defeats for the armies of the dictators. The armies of both Napoleon and Hitler were far superior to the Russians. It was the conditions in which the battles were fought that resulted in these defeats. Russian winters are often held responsible for the fate of these armies. In reality, it was the ill-preparedness and bad judgment of both Napoleon’s and Hitler’s men that caused them the humiliating defeats. They were very well trained men but they were trained in benevolent conditions of France and Germany. This time, the battle was in completely different and extreme conditions, and they could not cope with it.
The failure of credit risk models during the financial crisis 0f 2007-08 could be related to the fate of both the French and German armies. The models were built and trained in a benevolent economic environment and were ill-prepared to deal with extreme economic conditions at the time. Additionally, there were series of bad judgments by the executives at the financial firms that resulted in total economic collapse.
The moral of the above stories is that one has to keep a close tab on a change in conditions in the currently prevalent environment and training environment. The Basel III accord has paid a significant attention towards monitoring portfolio on a regular basis for a good reason. The population stability index (PSI) is one such index that helps risk managers in performing this task for retail credit scorecards.
Population Stability Index (PSI) – Our Banking Case Continues
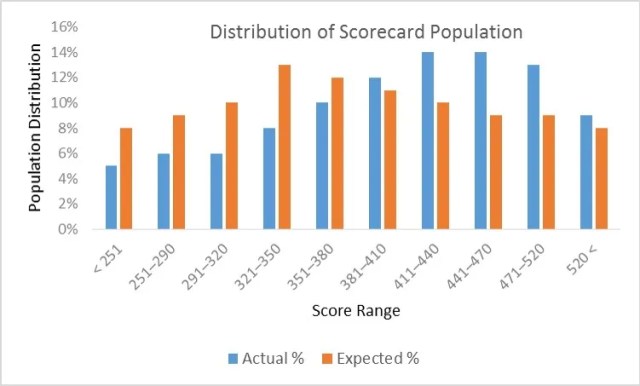
You are the chief-risk-officer at CyndiCat bank. It’s been a couple of years since your team, in your supervision, has built the auto-loans credit scorecard. Since then the overall risk assessment process for the bank has improved significantly. Though being a prudent risk manager you have asked your team to regularly compare the population for which the scorecard was built and the existing through-the-door population (applicants for auto loans). A good place to start this comparison is by checking how two populations are distributed across the risk bands created through the scorecard. The following is a representation for the latest quarterly comparison your team has performed against the benchmark sample. Here Actual %’ is the population distribution for the latest quarter and ‘Expected %’ is the population distribution for the validation sample (a.k.a. benchmark sample).
Comparing two populations visually is a good place to start. The current population seems to have shifted towards the right side of the graph. To a small extent, this is expected since scorecards often influence the through-the-door population as the market starts reacting to the approval strategies of the bank. However, the question we need to ask is whether this a major shift in the population? Essentially, you are comparing two different distributions and could use any goodness-of-fit measure such as Chi-square test. However, the population stability index is an industry-accepted metric that presents some convenient rules of thumb for the same. The population stability index (PSI) formula is displayed below (refer to ‘Credit Risk Scorecards’ by Naeem Siddiqui)
Again like the weight of evidence and the information value, PSI seems to have it’s root in information theory. Let’s calculate the population stability index (PSI) for our population (we have already seen a histogram for this above).
| Score bands | Actual % | Expected % | Ac-Ex | ln(Ac/Ex) | Index |
| < 251 | 5% | 8% | -3% | -0.47 | 0.014 |
| 251–290 | 6% | 9% | -3% | -0.41 | 0.012 |
| 291–320 | 6% | 10% | -4% | -0.51 | 0.020 |
| 321–350 | 8% | 13% | -5% | -0.49 | 0.024 |
| 351–380 | 10% | 12% | -2% | -0.18 | 0.004 |
| 381–410 | 12% | 11% | 1% | 0.09 | 0.001 |
| 411–440 | 14% | 10% | 4% | 0.34 | 0.013 |
| 441–470 | 14% | 9% | 5% | 0.44 | 0.022 |
| 471–520 | 13% | 9% | 4% | 0.37 | 0.015 |
| 520 < | 9% | 8% | 1% | 0.12 | 0.001 |
| Population Stability Index (PSI)= | 0.1269 | ||||
The last column in the above table is what we care for. Let us consider the score band 251-290 and calculate the index value for this row.
The final value for the PSI i.e. 0.13 is the sum of all the values of the last column. Now the question is how to interpret this value? The rule of thumb for the PSI is displayed below
| PSI Value | Inference | Action |
| Less than 0.1 | Insignificant change | No action required |
| 0.1 – 0.25 | Some minor change | Check other scorecard monitoring metrics |
| Greater than 0.25 | Major shift in population | Need to delve deeper |
The value of 0.13 falls in the second bucket which indicates a minor shift in population from the validation or benchmark sample. These are handy rules to have. However, one must ask, how is this population shift going to make any difference in the scorecard? Actually, it may or may not make any difference. Each score band of a scorecard has an associated bad rate or probability of customers not paying off their loans. For instance, score band 251-290 in our scorecard has a bad rate of 10% or one customer out of the population of 10 in this score band won’t service his/her loan. The population stability index simply indicates changes in the population of loan applicants. However, this may or may not result in deterioration in performance of the scorecard to predict risk. Nevertheless, the PSI indicates changes in the environment which need to be further investigated through analyzing the change in macroeconomic conditions and overall lending policies of the bank.
Sign-off Note
The population stability index is one of the metrics to keep a check on changing conditions – however, the idea is clear that one has to capture robust metrics to keep a close look on the ever changing economic winds to prevent a crash landing. On the other side, Russian winters did change the history of the planet for better – I guess change is not always for bad.
This was a bit of a detour from our previous article on books to learn probability and Bayesian statistics. Hopefully, you have got a chance to check out some of the books mentioned in the earlier article, see you soon with the second part of that article.


The following are some really important points raised by a reader on LinkedIn. I completely agree with all the points and believe analysts should keep them in mind while using PSI.
———————
by Michael Mout
The author does not point out that PSI has a number or conditions on it.
Primarily, it is very sensitive to sample size and the number of score bands. A PSI value of .2+ for 5 score bands may not mean the same PSI value for 20 score bands.
Also, the PSI is usually based on some baseline and it is just as important to track the ongoing trend pf the PSI as its absolute value. For example, the baseline may be taken from a time where scores were low and they have increased over time so that a PSI of .25 may become the new standard. One solution is to change the baseline to reflect the new reality, but that does not necessarily reflect the population on which the model was developed.
Just as important is that the PSI dictates that something has happened to the underlying population and the model owner needs to dig further into variable level results. This is where a complex model can get very tricky. If the model is linear with all the underlying predictors, one can look at the individual changes in variable distribution (VLM – Variable Level Monitoring) to see what is driving the overall score change. This often turns out to be the result of new marketing campaigns, expanded geographies or less (or more) restrictions on the TTD (Through The Door) population.If the underlying population is more complex (interaction variables, non-monotonic transformations, complex trees, NN, …) then this VLM level monitoring is much less straightforward.
Finally, PSI is merely an early warning sign. It does not mean that the model needs to be redeveloped, only that the underlying population has changed and that the model MAY NOT still be working. If actual performance has a short window then the performance can be readily verified, if not, then some sort of early performance (like 30 or 60 days past due for credit models or early sales for revenue models) should be identified which should also be rank ordered by the model. This can help verify if the model appears to be still working or not. If not, redevelopment should be investigated.
——–
Firstly, great post regarding PSI.
I would love to read all the comments for the article you posted on LInkedIn. Can you provide me the name of the group?
Thanks and Keep posting!
Hi, can the shift in population be interpretated as a change in distribution between the development dataset and new data set? So assuming that the development dataset is normally distribution. Now the new dataset might be have a skewed distribution to the left ( lower vie bins have higher count)?
Thanks for this very useful banking series. Thanks also for posting the conditions under which PSI works. It is good to point out the features and nature of the indicator as all statistical indicator have their own strengths and limitations.
By the way, where is part 5? don’t want to miss it.
Hi, You could find Part 5 at the following link, Enjoy!
Thanks for the article, however, it would be even better when this website would not show any image of past dictators, esp. Hitler. There is no need to further add pictures of their portraits to the world. If pictures in this context are needed then they would better show the victims of all those crimes.
I am sorry if this has hurt your sentiments in any possible way. I can totally understand your angst and disgust for dictators and Hitler in particular. As you may have noticed while reading the article that the attempt was not at all to glorify their heinous behavior. Rather, it is an attempt to avoid mistakes like credit crisis. I hope you understand.
Hi Roopam,
I’m inviting friend to look for PSI in your page,
could you do a painting of Napoleon instead of Hitler?
Please consider it 🙂
I must say, I initially tried painting Napoleon for this article but I found it difficult with my limited artistic skills :(. Let me though give it another shot. In the mean time please bear with me.
Changed the painting 🙂
thank you so much your help. If you don not mind can I ask you a question?
about psi formula, why we have to multiply LN(A%/B%) ??
is there a special reason why we have to use ln? or we just use ln because we have to make psi more than 0?
thank you so much 🙂
please tell what does it mean if the PSI is increasing over time?
PSI increasing over time means that the historic sample/population used for development of scorecard is not the same as the current population used to score. A high value of PSI means development sample is no longer representative for scoring the current applications. Hence, the scorecards might require either re-calibration or redevelopment.
please can you tell me how to calculate for instability index. like having annual data for the production of a single crop say cotton. having such data, how will i calculte an instability indices for each year. thanks for your anticipated help
Hi Roopam,
Could you tell me how to calculate PSI if de Actual% or Expected% for a band is 0%?
Thanks a lot!
Hi, PSI bins are not allowed to have 0 in the actual or the expected population. 0 can only happen if either your bins are of inappropriate width or the sample size for expected population is small. In the first case, change the width of the bins to avoid 0s. In the second case, wait for more sample.
Hi Roopam, liked your articles on model/ scorecard development. Concepts are very well explained. Are you planning/ or you have already an article on Scorecard calibration ?
Again all your articles are superb and easy read.
thanks.
Had few Questions on PSI. It would be great help if someone can answer these:
1) What is the effect of number of buckets on PSI thresholds? What will be PSI limits for 20 or 5 buckets?
2) Can PSI for categorical variables be calculated similar to numerical variables?
3) What is the math behind the PSI calculation?
Why Actual% does not add up to 100%. I think it is 97%. Is it just because of round issue?
Yes, I had to remove decimals for the page formatting but it will add up to 100% for the real data.
Hi,
I am developing a psi logic for Banking case analysis.I have some queries on it
1. Is PSI calculated on all the fields used for all the fields that is used for capturing the customer information?
2. If i calculate actual% on the data set of 2017 on field cibilScore, How should i calculate expected %?
3. Is there any industry standard for expected % that we can refer to for feeding in the expected value to the model?
very interesting article and nice explanation of test. Please clarify whether the actual and expected rate are the bad rates?
No, they are population distribution per bucket. Here, ‘actual’ is the current through-the-door (TTD) population and ‘expected’ is the TTD at for the development population.
Hi Roopam,
Thank you very much for your explanation. I am wondering is there any other metric that can detect data population shift? I found many research paper in “covariate shift”. Researchers train a classifier to tell whether there is a significant shift or not. Do you think that might be helpful in real-world banking business? Thank you!
There can be many metrics actually to measure population shift including Chi-Square test etc. PSI is the commonly used metric in the industry. The covariate shift is a much wider measure that detects the overall difference between the development and production data. Yes it can be used to measure population shift as well.
if Actual% is 0,PSI=?
It is undefined and PSI breaks down at 0 and infinity. However, these are impossible scenarios since the score buckets are usually created as the decile of the original scores.
Roopam,
I have studied PSI for my Phd thesis and I think it would be pretty beneficial in terms of understanding properties of PSI and some additional questions people are askin in the comments. Let me know your thoughts.
Thanks.
Please check out the link below to see my thesis.
https://www.linkedin.com/feed/update/urn:li:activity:6425031171561844736
Thanks, Bilal. If you wish to write a post on PSI based on your thesis, I will be more than happy to host it on YOU CANalytics. Cheers!
Hi Roopam, how are you?! Long time! First of great article! and needless to say, as always 🙂 !!, as I was reading through the internet to know all about PSI, think this might stop my further research for the time being because few comments helped in some other corrections too, although I have one confusion now that when thought of the development and current populations.
Currently I am working on an ad-hoc project wherein we are required to validate the current geography’s bureau scorecard and if found reliably consistent with the banks retail population, would be used to further model PDs and recalibrate the current TTC scale in place.
So lets say we have 5years of data and we build score buckets based on 1st years score rankings on its population and for the following years, we continue with the same buckets achieved here. Now when I am comparing 1st and 2nd population, its quite clear, my question arises for further comparisons, that are we supposed to still think of 1st years population as development and 3rd year as current, because we want to see the population shift in the buckets created which originally came from the 1st population ranked score data, or 2nd as new development data and 3rd as current because we already noticed 1st to 2nd transition, while ignoring the fact that 2nd population most probably would have its own and differently ranked and differently sized buckets due to increase in the population, which are not being adopted to, keeping in mind, scores are coming from the same bureau authority and of course application of the same scorecard model in application over these years.
Hi Rahul, good to hear from you! Let’s discuss this over a call. Cheers.
Hi Roopam – your article is an incredible resource in explaining PSI!
I really appreciate that you changed the image from a painting of Hitler to a painting of Napoleon.
Unfortunately it is still used within the metadata of this page as the meta og:image, though. This means that when the url is shared on anything that tries to fetch a thumbnail and description, the hitler image still shows.
Your article has become such a useful resource in explaining PSI that myself and colleagues have been known to share it around quite a bit, so this has actually popped up a number of times for us.
Please take a look into this (hopefully just a matter of updating a field in WordPress), I appreciate it!
Thanks, Tim. Changed that too – please check.
Perfect, thanks!
great content and great picture!
Hi Roopam,
I wanted to know how to deal with a situation where the population has become 0 for a particular score band in the current population.
Let me know your thoughts.
Thanks!.
Hi Roopam,
Thank you for great explanation of PSI!
I have a question about that if you could answer I really appreciate it!
I am wondering that how should we choouse data sets to calculate PSI. Yes, the answer is clear, the first one is the train data set that has been used in the model development and the other one is new population sample.
But, in my case, I have applied “Robust Scaling Technique” to train data set before run the model. I am confused that, in PSI, which data set should I use to compare with new population sample.
-The train data set that is used in the model development without Robust Scaling (If you suggest that, I will not apply robust scaling to new population sample, please correct me if I’m wrong).
-The train data set that is used in the model development with Robust Scaling (If you suggest that, I will apply robust scaling to new population sample, please correct me if I’m wrong).
Thank you for your help
Best
Btw, I’ve tried both way and found different features which exceed psi threshold (0.2). I am not sure which way is correct to test PSI values.
Hi Roopam,
This is by far the best article on PSI i have come across. It is so well articulated and simple to understand. I cant thank you enough for this. I work in a model validation field. I have small question about the number of score bands in PSI.
You mentioned that “it is very sensitive to sample size and the number of score bands. A PSI value of .2+ for 5 score bands may not mean the same PSI value for 20 score bands”. So what is the apt number of score bands to calculate the PSI? usually i have heard it is 10, but people do use 20 or less as well, not sure what difference it makes, if you can explain please? Also, can we define the score bands based on other than 10% of the population? and why ?