Sugar Cane Juice and ARIMA – by Roopam
For the last couple of articles, we are working on a manufacturing case study to forecast tractor sales for a company called PowerHorse. You can find the previous articles on the links Part 1 and Part 2. In this part, we will start with ARIMA modeling for forecasting. ARIMA is an abbreviation for Auto-Regressive Integrated Moving Average. However, before we learn more about ARIMA let’s create a link between…
ARIMA and Sugar Cane Juice
May and June are the peak summer months in India. Indian summers are extremely hot and draining. Summers are followed by monsoon rains. It’s no wonder that during summers everyone in India has the habit of looking up towards the sky in the hope to see clouds as an indicator of the arrival of monsoons. While waiting for the monsoons, Indians have a few drinks that keep them hydrated. Sugar cane juice, or ganne-ka-ras, is by far my favorite drink to beat the heat. The process of making sugar cane juice is fascinating and has similarities with ARIMA modeling.
Sugar cane juice is prepared by crushing a long piece of sugar cane through the juicer with two large cylindrical rollers as shown in the adjacent picture. However, it is difficult to extract all the juice from a tough sugar cane in one go hence the process is repeated multiple times. In the first go, a fresh sugar cane is passed through the juicer and then the residual of the sugar cane that still contains juice is again passed through the juicer many times till there is no more juice left in the residual. This is precisely how ARIMA models work
. Consider your time series data as a sugar cane and ARIMA models as sugar cane juicers. The idea with ARIMA models is that the final residual should look like white noise otherwise, there is juice or information available in the data to extract.
We will come back to white noise (juice-less residual) in the latter sections of this article. However, before that let’s explore more about ARIMA modeling.
ARIMA Modeling
ARIMA is a combination of 3 parts i.e. AR (AutoRegressive), I (Integrated), and MA (Moving Average). A convenient notation for ARIMA model is ARIMA(p,d,q). Here p,d, and q are the levels for each of the AR, I, and MA parts. Each of these three parts is an effort to make the final residuals display a white noise pattern (or no pattern at all). In each step of ARIMA modeling, time series data is passed through these 3 parts like a sugar cane through a sugar cane juicer to produce juice-less residual. The sequence of three passes for ARIMA analysis is as follows:
1st Pass of ARIMA to Extract Juice / Information
Integrated (I) – subtract time series with its lagged series to extract trends from the data
In this pass of ARIMA juicer, we extract trend(s) from the original time series data. Differencing is one of the most commonly used mechanisms for extraction of trends. Here, the original series is subtracted from it’s lagged series e.g. November’s sales values are subtracted from October’s values to produce trend-less residual series. The formulae for different orders of differencing are as follow:
| No Differencing (d=0) |  |
| 1st Differencing (d=1) |  |
| 2nd Differencing (d=2) |  |
For example, in the adjacent plot, a time series data with a linearly upward trend is displayed. Just below this plot is the 1st order differenced plot for the same data. As you can notice after 1st order differencing, trend part of the series is extracted and the difference data (residual) does not display any trend.
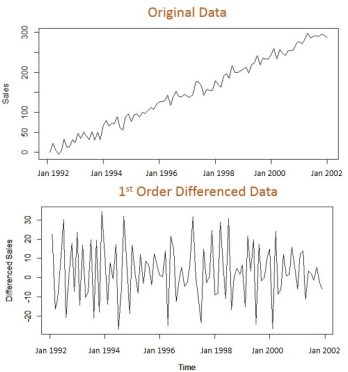
The residual data of most time series usually become trend-less after the first order differencing which is represented as ARIMA(0,1,0). Notice, AR (p), and MA (q) values in this notation are 0 and the integrated (I) value has order one. If the residual series still has a trend it is further differenced and is called 2nd order differencing. This trend-less series is called stationary on mean series i.e. mean or average value for series does not change over time. We will come back to stationarity and discuss it in detail when we will create an ARIMA model for our tractor sales data in the next article.
2nd Pass of ARIMA to Extract Juice / Information
AutoRegressive (AR) – extract the influence of the previous periods’ values on the current period
After the time series data is made stationary through the integrated (I) pass, the AR part of the ARIMA juicer gets activated. As the name auto-regression suggests, here we try to extract the influence of the values of previous periods on the current period e.g. the influence of the September and October’s sales value on the November’s sales. This is done through developing a regression model with the time-lagged period values as independent or predictor variables. The general form of the equation for this regression model is shown below. You may want to read the following articles on regression modeling Article 1 and Article 2.
AR model of order 1 i.e. p=1 or ARIMA(1,0,0) is represented by the following regression equation
3rd Pass of ARIMA to Extract Juice / Information
Moving Average (MA) – extract the influence of the previous period’s error terms on the current period’s error
Finally, the last component of ARIMA juicer i.e. MA involves finding relationships between the previous periods’ error terms on the current period’s error term. Keep in mind, this moving average (MA) has nothing to do with moving average we learned about in the previous article on time series decomposition. Moving Average (MA) part of ARIMA is developed with the following simple multiple linear regression values with the lagged error values as independent or predictor variables.
MA model of order 1 i.e. q=1 or ARIMA(0,0,1) is represented by the following regression equation
White Noise & ARIMA
Oh, how I miss the good old days when television was not on 24×7. For the good part of the day the TV used to look like the one shown in the picture – no signals just plain white noise. As a kid, it was a good pass time for my friends and me to keep looking at the TV with no signal to find patterns. White noise is a funny thing, if you look at it for long you will start seeing some false patterns. This is because the human brain is wired to find patterns, and at times confuses noises with signals. The biggest proof of this is how people lose money every day on the stock market. This is precisely the reason why we need a mathematical or logical process to distinguish between a white noise and a signal (juice/information). For example, consider the following simulated white noise:
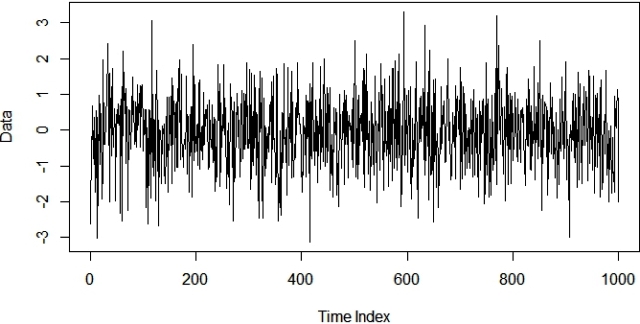
If you stare at the above graph for a reasonably long time you may start seeing some false patterns. A good way to distinguish between signal and noise is ACF (AutoCorrelation Function). This is developed by finding the correlation between a series of its lagged values. In the following ACF plot, you could see that for lag = 0 the ACF plot has the perfect correlation i.e. ρ=1. This makes sense because any data with itself will always have the perfect correlation. However as expected, our white noise doesn’t have a significant correlation with its historic values (lag≥1). The dotted horizontal lines in the plot show the threshold for the insignificant region i.e. for a significant correlation the vertical bars should fall outside the horizontal dotted lines.
There is another measure Partial AutoCorrelation Function (PACF) that plays a crucial role in ARIMA modeling. We will discuss this in the next article when we will return to our manufacturing case study example.
Sign-off Note
In this article, you have spent your time learning things you will use in the next article while playing your role as a data science consultant to PowerHorse to forecast their tractor sales.
In the meantime, let me quickly check out of my window to see if there are any clouds out there………. Nope! I think there is still time before we will get our first monsoon showers in Bombay for this year – need to keep my glass of sugar cane juice handy to fight this summer.
wonderful Explanation!
Hi Roopam
Nice analogy. This really help in clear understanding of the technical concepts. I enjoyed reading your blogs. Great work!
I love the simplicity in your explanation
Hi,
I am learning analytics techniques and your blog is very helpful.
About ARIMA -: I got some understanding of its parameters p – lags of auto regression of previous observations, d – used to converted input time series data into stationary by differencing for d terms,
But has doubts for q – moving average of errors.
Lets say we have time series data as y1, y2, y3, y4….. yn. Our ARIMA model is (0,0,1) i.e. q =1.
Suppose values calculated using ARIMA(0,0,1) are appears as Y1, Y2, Y3, Y4…..
I would like to know how first element Y1 is calculated.
As per understanding, Y1 = c + theta(e1) where e1 is the first error.
My question is – error is calculated as difference between actual value (y1) and forecasted value (Y1) and here forecasted value- Y1 – is yet to be calculated so how can error is calculated in MA part of ARIMA.
Thanks a lot for your time
With regards
ND.
That’s a good question.This is essentially an iterative calculation. Here, the error or residual (a better term) is left after AR and I terms are extracted from the series. The MA term then tries to model the pattern in this residual, if any, to make the final error looks like white noise.
Heyi Roopam,
I have read you blog for the first time and the only word I have to say is mind blowing.
Cleared lot of basic confusion for which no answer is available in any book.
Great Work.
Hi Roopam,
You make learning analytics more fun! Thanks!
David
we are working on a long range forecasting project for their sales in 2017 using SARIMAX. We did the forecasting in SAS and now we have to migrate to R.
The issue that we are facing is a difference in Comp Percentages of sales between the SAS model and that in R.
In SAS we have fixed on the optimum p,d,q values by running the ARIMA on sales and then the lags for all the exogenous variables are fixed based on the correlation results. We also manually change the differencing orders to improve the stability of the model.
While converting the codes to R, we used the p,d,q values that were inputs to SAS. The ACF and PACF graphs show that the residuals are not within the limit and hence we had change the p,d,q values by running the ARIMA of sales in R. The lags for all the exogenous variables are fixed based on the correlation results. The results that I get from this model is completely different from the results that I get in SAS.
The problem is that R automatically differences the exogenous variables with the ‘d’ value of the model. We have tried to match the SAS model and R model by using the same differencing orders (i.e ‘d’ value of sales is used to difference all the variables) even then the results did not match.
Could you please help us understand the reason for this or point us to someone who could.
Hi Gaurav
We are going to use ARIMAX for multivariate Time Series model for a pharma drug sales forecast.
Would like to understand few things from you.
Regards
Hi,
Roopam…Really great articles .
I am new to analytic and trying to understand the MA model. I donot able to understand that why we take previous errors to forecast values in MA model.
Really appreciate if you can make understand me the logic behind that.
The most practical answer is that it works to have MA terms in the model for making better forecasts. The underlining assumptions here is that there are periods of higher and lower uncertainty (error terms) in a time series and they are periodic in nature. Hence, MA terms capture this periodic phases of fluctuating uncertainty.
Hi Roopam,
Very nice explanation about ARIMA.
My question is , though we are doing difference as part of Integrated (I) its called integrated.
May I know reason why its called so and why not ARDMA ?
Thanks in advance…
That’s a good question. Unfortunately, I don’t know the answer. If you come across some good explaination please let me know.
Hi, I just discovered this blog and I think it is a very good place to lear Time series analysis.
To answer your question, why is ARIMA and not ARDMA, think first of the model ARMA. This model requires the input data to be already stationary. So you have to perform differencing before ARMA model.
In ARIMA, this operation is integrated into the model i.e the model does it for you – so you can feed into the model a non-stationary data and the model will transform it for you.
I love your analogies. It’s a joy to read your blog. Keep up the good work!
Hi this a very very wonderful post, thank you!
Hi Roopam ,
i have a doubt what if we have a daily data and we wanna take care of the weekend values or the holidays then what should be the approach,and for the daily data how do you write the ts function i am confused whether the freq should be 365 ?
Weekends will be weekly seasonality in your data if the sales peak over the weekend. However, if weekends are off then considered 5-day week and then run the model without using zero productivity on the off days.
Nice one.
However, the picture is gross.. I mean, the person does not seem to use gloves while handling the juice, and perhaps he is drenched in sweat.
I know it’s filthy, I was hoping someone will point that out :-). This is precisely the reason why one can’t drink the juice everywhere. There are a few places where they keep it hygienic. However, by and large, they are ruining a great product that has enormous potential.
Ahem…so the chef cooking your dinner at the suave restaurant you like to go is wearing gloves in a hot kitchen, holding a hot stove and is not sweating at all.
The chemicals getting dispensed of the latex gloves is much more harmful than the natural odor of a human hand. In the pretext of cleanliness, the western world has synthesized our every day life and that causes more diseases than the diseases that occurs naturally. Also the body has defence mechanism to fight the germs it kinows .. so shut your stinky mouth
Thanks for these posts – fantastic resource to learn about ARIMA and time series!
such clarity of thoughts
i have yet to meet someone who explains these concepts better than you :),
I often visit your blog and have noticed that you don’t update it often. More frequent updates will
give your site higher authority & rank in google. I know that writing posts takes a
lot of time, but you can always help yourself with miftolo’s tools which will shorten the time of creating an article to a couple of seconds.
Wonderful explanation! You have a knack to simplifying things. Thank you so much for this great explanation!
Simply Wonderful and simple explanation.Helped clear my doubts…Please keep posting.
i have never understood ACFs better! thank you so much. Keep publishing such intiutive artices and of course the editing is amazing with easy to grasp sentence framing.