Let us continue with our inadvertently started tradition of separating the articles on cluster analysis with a different topic to make them form perfect clusters. This time, I am going to discuss iterative calculation in between articles on our running series on cluster analysis and customer segmentation for telecom.  Though I must say we are going to use concepts discussed in this article in the next article on cluster optimization and customer segmentation. Coming back to iterative calculation, almost all data mining and machine learning algorithms use iterative calculation methods to arrive at the solution for curve fitting, classification, and prediction. Let us try to understand how Archimedes devised a strategy to estimate the value of π through iterative calculation more than two thousand years ago.

Archimedes of Syracuse

Archimedes – by Roopam

Eureka! This is the word most of us associate with Archimedes who lived between 287–212 BC. Eureka! Archimedes screamed in exhilaration in his bath tub upon discovering the phenomenon of buoyancy, the upward force exerted by a fluid on the immersed object. Eureka is the word associated with the moment of joy experienced through discovery or invention. Archimedes was certainly a Eureka man. During the Renaissance (14th–17th century AD) the concepts known to Archimedes were independently discovered. Imagine the surprise when the contents of Archimedes manuscripts were revealed in 1906 and it was appreciated that he had discovered the Renaissance concepts more than thousand years before! Archimedes was indeed a man who was centuries ahead of his time.

Isaac Newton and Gottfried Leibniz are credited with the invention of ‘calculus’ (the mathematical study of change)  in the 17th century. However, the concept of limits that is at the heart of calculus was used by Archimedes to estimate the value of π (Pi).  The famous π is an irrational number that has the value 3.141592653589793238 … (this number will go on till eternity or infinity).

Limits of π (Pi) – Archimedes’ Genius

Let us try to understand the genius of Archimedes through his estimation of the limits of π. Let us start by drawing two squares one inside and the other outside of the circle as shown in the adjacent figure.  It is easy to notice that the area of the circle is greater than the area of the inner square. Also, the area of the outer square is greater than the area of the circle. This relationship will also hold for the perimeters of the inner and outer squares and circumference of the circle. Remember, the perimeter of a square is the sum of the length of all the sides of a square and circumference is the length of the boundary of a circle.

Moreover, recall from the high-school math that circumference of a circle is equal to πd i.e. π times diameter of the circle. It is easy to see that for a circle with the diameter of one (i.e. d=1), the circumference is just π.

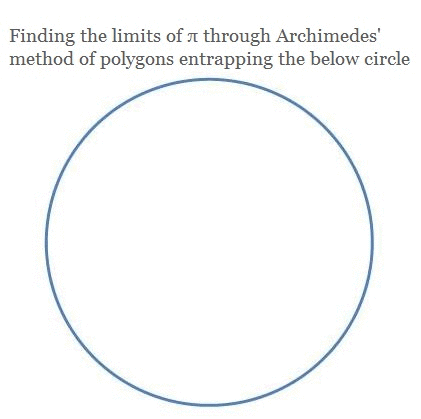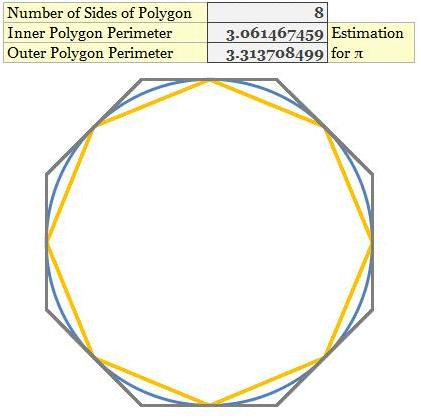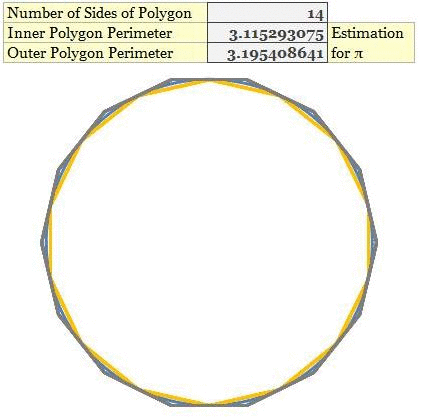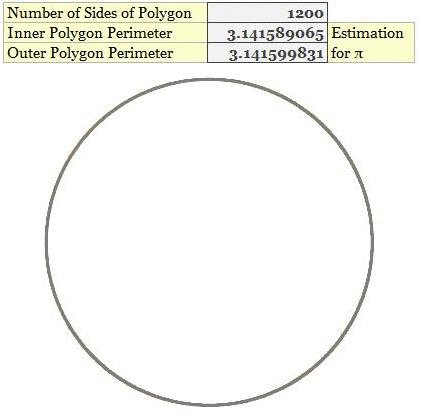
Now it is time to generalize our above findings. A square is a polygon with 4 sides. The above relationship about squares and the circle is true for all the polygons drawn inside and outside a circle. This general relationship can be depicted as

Perimeter of the Inner Polygon < π < Perimeter of the outer Polygon

You might appreciate that finding the value of perimeter of a polygon is much simpler than finding the value of π. Just find the perimeter of the inner and outer polygon and you have found the upper and lower limits for π. The stroke of genius for Archimedes was his realization that as the number of sides of polygons was increased he could capture the value of π to a greater precision. Theoretically, if Archimedes had constructed a polygon with an infinite number of sides he would have produced the exact value of π (sounds like calculus, isn’t it?). This same phenomenon is captured in the animation below.

← Download the Excel to play around with these polygons yourself (I find it good fun)

Archimedes had painstakingly calculated the limits of π using polygons with 96 sides. I have shown this in the above animation as a tribute to Archimedes. You might have noticed that with 96 sides the value of π has converged to just first two decimal places i.e. 3.14 (remember using this number in the high-school math). This was a phenomenal discovery by Archimedes but had its own limitations. For instance, Archimedes’ method converges to the value of π very slowly.  Notice the last slide in the animation, even with a polygon with 1200 sides the value of π has converged to just fourth decimal place i.e. 3.1415.

An Important Problem in Mathematics

Using Archimedes method, it will take eternally long time to learn the 10 trillion digits of π (the current record for finding the largest number of digits of π on a personal computer). This is a good place to appreciate an important problem in modern mathematics, computer science, and machine learning.  The idea is not just to find an algorithm that converges to the right value but also fast. In the context of π, it is an apt time to introduce an equation suggested by another genius Srinivasa Ramanujan. Evaluate the following equation for π suggested by him

It’s beautiful, isn’t it? Ok I agree, it is incomprehensible but it does converge to the value of π and that too really fast. All the modern formulas for estimating the value of π use Ramanujan’s method in some form or other. This formula gives the right value of π to 14 decimal places in just 2^nd iteration i.e. k = 1. This is a major improvement on our estimation of π using the Archimedes’ method.

Sign-off Note

You must have noticed my penchant for sketching as I try to include a sketch in all my blog posts. I really enjoy drawing these sketches. I have equally enjoyed creating Archimedes’ method of the polygon on an excel spreadsheet which is used in the above animation. I guess I am a visual mathematician.

See you soon with the continuation of our telecom case study in the next article.